
If the graph of the quadratic function \(y = ax^2 + bx + c \) crosses the x-axis, the values of \(x\) at the crossing points are the roots or solutions of the equation \(ax^2 + bx + c = 0 \). Graph of y = ax 2 + bx + c Finding points of intersection Roots of a quadratic equation ax 2 + bx + c = 0

The turning point lies on the line of symmetry. The graph of the quadratic function \(y = ax^2 + bx + c \) has a minimum turning point when \(a \textgreater 0 \) and a maximum turning point when a \(a \textless 0 \). Excellent activity where quadratic functions are matched to graphs.All quadratic functions have the same type of curved graphs with a line of symmetry. More on quadratic functions and related topicsįind Vertex and Intercepts of Quadratic Functions - Calculator: An applet to solve calculate the vertex and x and y intercepts of the graph of a quadratic function.ĭerivatives of Quadratic Functions: Explore the quadratic function f(x) = ax 2 + b x + c and its derivative graphically and analytically. Ĭontinue to (Find quadratic Function given its graph)Ĭontinue to (Explore the product of two linear functions) Ī) Use the applet window to check the y intercept for the quadratic functions in the above example.ī) Use the applet window to check the y intercept is at the point (0,c) for different values of c. The graph of h has a y intercept at (0,4). The graph of g has a y intercept at (0,1). The graph of f has a y intercept at (0,-3). Įxample: Find the y intercept of the graph of the following quadratic functions.Ī) f(0) = -3. The y intercept of the graph of a quadratic function is given by f(0) = c. How many x -intercepts does the graph of f(x) have ?ĭ - y intercepts of the graph of a quadratic function Use the analytical method described in the above example to find the x intercepts and compare the results.ģ) Use the applet window and set a, b and c to values such that b 2 - 4 a c 0. No x intercept for the graph of function in part c).ġ) Go to the applet window and set the values of a, b and c for each of the examples in parts a, b and c above and check the discriminant and the x intercepts of the corresponding graphs.Ģ) Use the applet window to find any x intercepts for the following quadratic functions. The graph of function in part b) has one x intercept at (1,0). One repeated real solutions x_1 = -b / 2a = -2 / -2 = 1 The graph of function in part a) has two x intercepts are at the points (1,0) and (-3,0). The solutions are given by the quadratic formulasĮxample: Find the x intercepts for the graph of each function given below It has one repeated solution when D is equal to zero. The above equation has two real solutions and therefore the graph has x intercepts when the discriminant D = b 2 - 4 a c is positive. The x intercepts of the graph of a quadratic function f given byĪre the real solutions, if they exist, of the quadratic equation Check that the graph opens down ( a 0 ) and that the vertex is at the point (1,-1) and is a minimum point.Ĭ - x intercepts of the graph of a quadratic function H and k can also be found using the formulas for h and k obtained above.Ī) Go back to the applet window and set a to -2, b to 4 and c to 1 (values used in the above example). Group like terms and write in standard form We now divide the coefficient of x which is -2 by 2 and that gives -1. The x and y coordinates of the vertex are given by h and k respectively.Įxample: Write the quadratic function f given by f(x) = -2 x 2 + 4 x + 1 in standard form and find the vertex of the graph. When you graph a quadratic function, the graph will either have a maximum or a minimum point called the vertex.
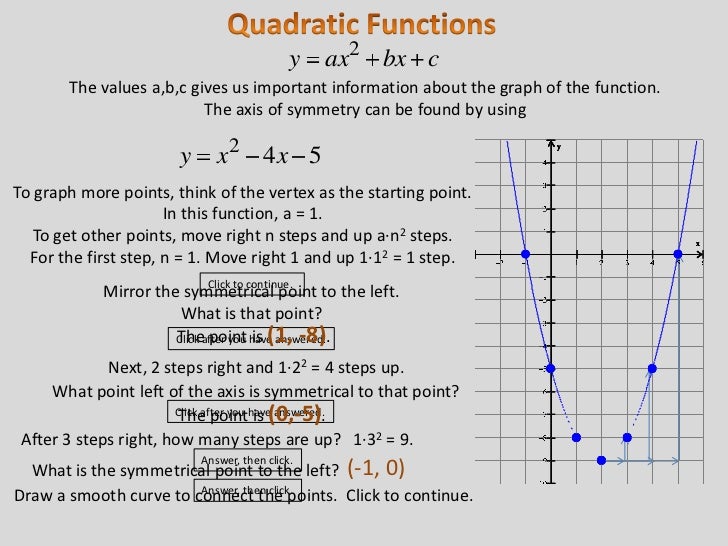
This is the standard form of a quadratic function with h = - b / 2a Let us start with the quadratic function in general form and complete the square to rewrite it in standard form.įactor coefficient a out of the terms in x 2 and xĪdd and subtract (b / 2a) 2 inside the parenthesesį(x) = a ( x 2 + (b/a) x + (b/2a) 2 - (b/2a) 2 ) + cį(x) = a ( x + (b / 2a) ) 2 - a(b / 2a) 2 + cį(x) = a ( x + (b / 2a) ) 2 - (b 2 / 4a) + c Where h and k are given in terms of coefficients a, b and c. You may change the values of coefficient a, b and c and observe the graphs obtained.Īnswers B - Standard form of a quadratic function and vertexĪny quadratic function can be written in the standard form Note that the graph corresponding to part a) is a parabola opening down since coefficient a is negative and the graph corresponding to part b) is a parabola opening up since coefficient a is positive.
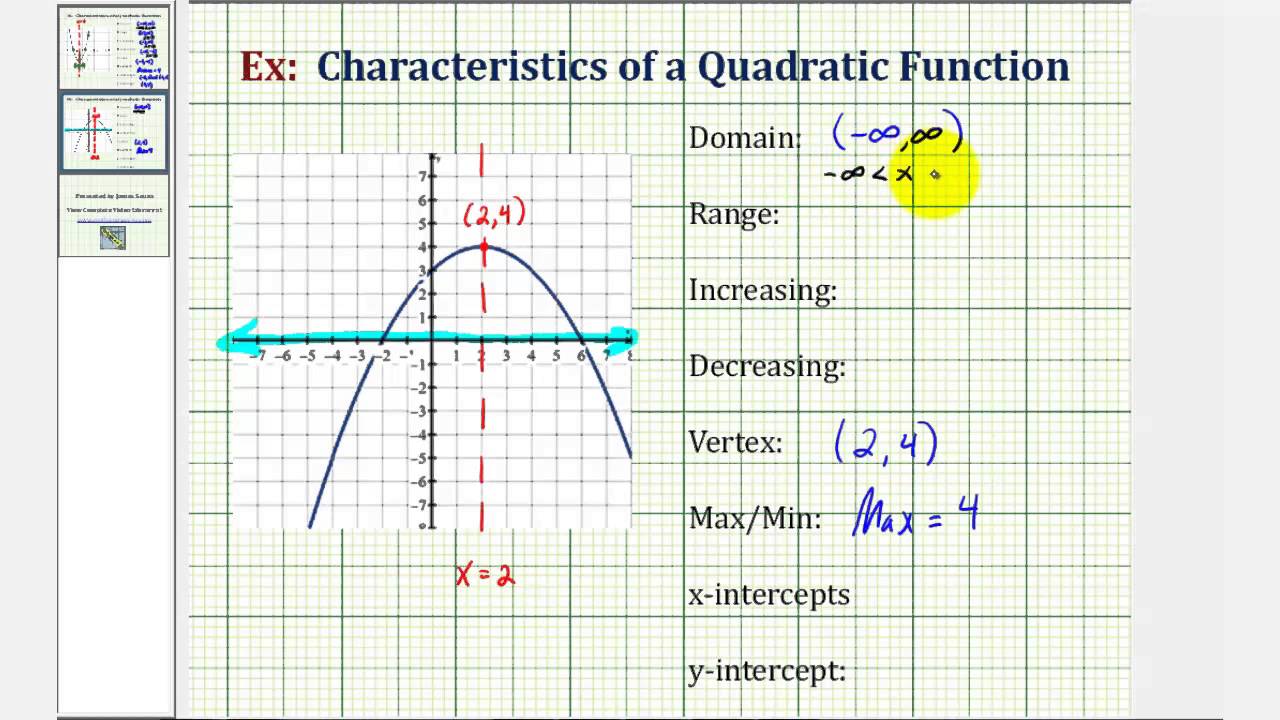
Use the boxes on the left panel of the applet window to set coefficients a, b and c to the values in the examples above, 'draw' and observe the graph obtained.


 0 kommentar(er)
0 kommentar(er)
